The File Drawer
Why is this the answer?
In my previous post I showed that the minimum inverse-probability weight in a simple random sample should be equal to the response rate of the survey. However, since simple random samples are basically non-existent in the real world, I need to work out the equivalent constraint for complex survey designs.
This post summarizes my progress so far towards doing that.
In the previous post I speculated that the constraint for \(i\)’s weight should be:
\[ \frac{FinalWeight_i}{SelectionWeight_i} >= RR_{total} \]
tl;dr that constraint is close but not exactly correct. I think I have now identified the correct constraint, but I haven’t yet proved it.
Does it work in practice?
After an hour of failing to work out an analytic proof, I thought it would be worth doing a simulation to see whether the claim is at least empirically true.
Let’s do a simple two-stage sample where households are randomly selected, then a respondent is randomly selected from that household. This means that people in larger households have a lower probability of selection. If you live alone there’s a 100% chance of selection conditional on your household being selected, whereas if you live in a two-person household your selection probability is 50%.
Conditional on being selected for the survey, rich people respond at 100% and poor people respond at 30%.
So after simulating that, I look at the response rate for the simulation (0.649) and the minimum value of the ratios of the final true weight to the selection weight (0.65). Not far off, but also not identical. So, it looks like my initial guess about the constraint might be on the right track but not exactly right.
Let’s try this a few more times and see whether it’s robust.
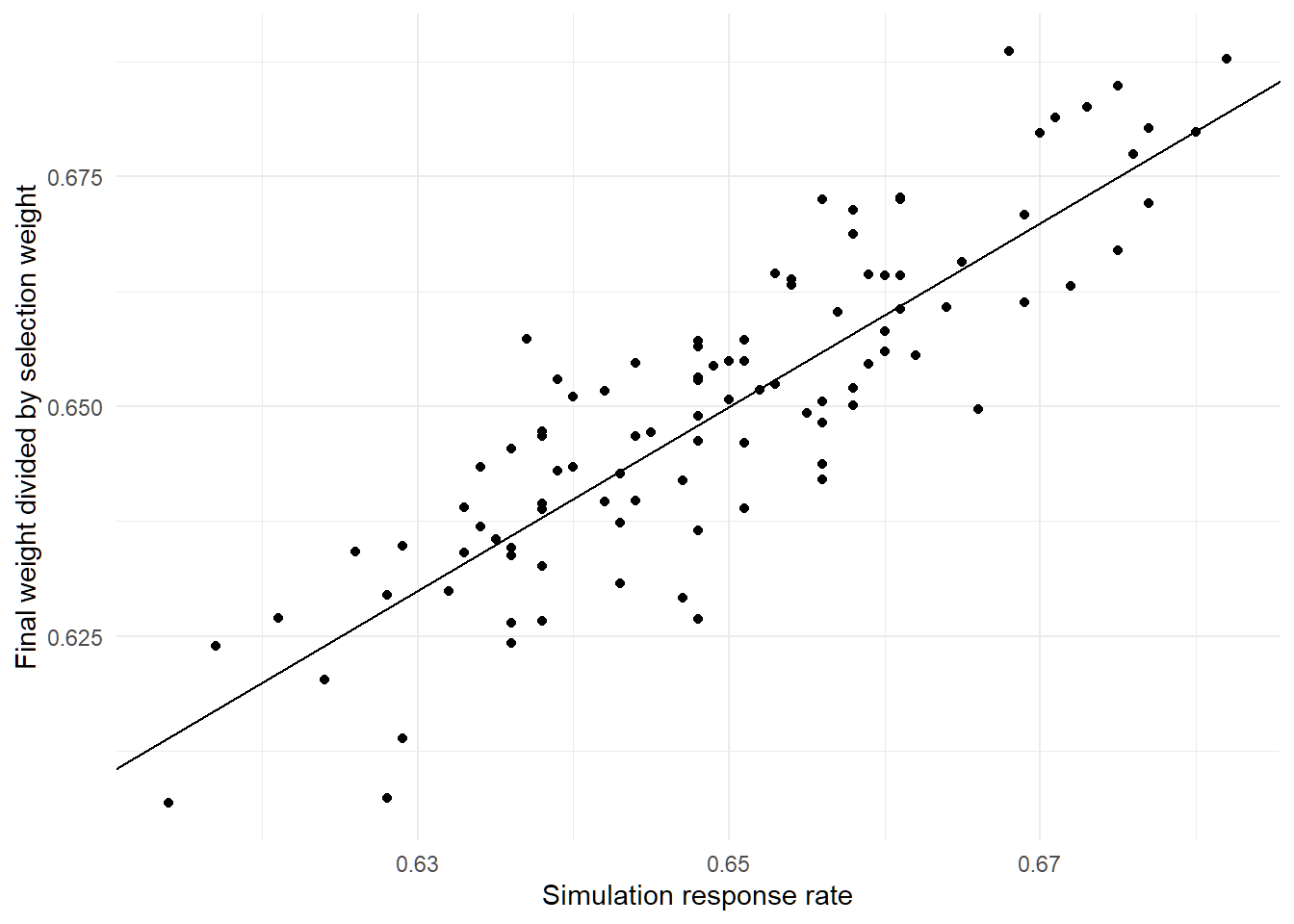
After 100 simulations, it’s clear that there’s a very strong relationship, but this not an exact match.
So what’s going on with those ratios? The mean of the scaled inverse-probability weights is always exactly 1 in the simulation as is the mean of the scaled selection weights.
However, the ratios themselves do not always have a mean of exactly one. In fact, on average, they are 0.0109 away from 1. But should we actually expect these ratios to be near one on average? If I simulate two random vectors and rescale them to both have a mean of 1, the average ratio of them isn’t usually anywhere near 1.
set.seed(1298)
A <- abs(rnorm(1000))
B <- abs(rnorm(1000))
A <- A / mean(A)
B <- B / mean(B)
mean(A/B)## [1] 4.292947OK, well what if I rescale the ratios so that they actually have a mean of 1 rather than just being close to that?
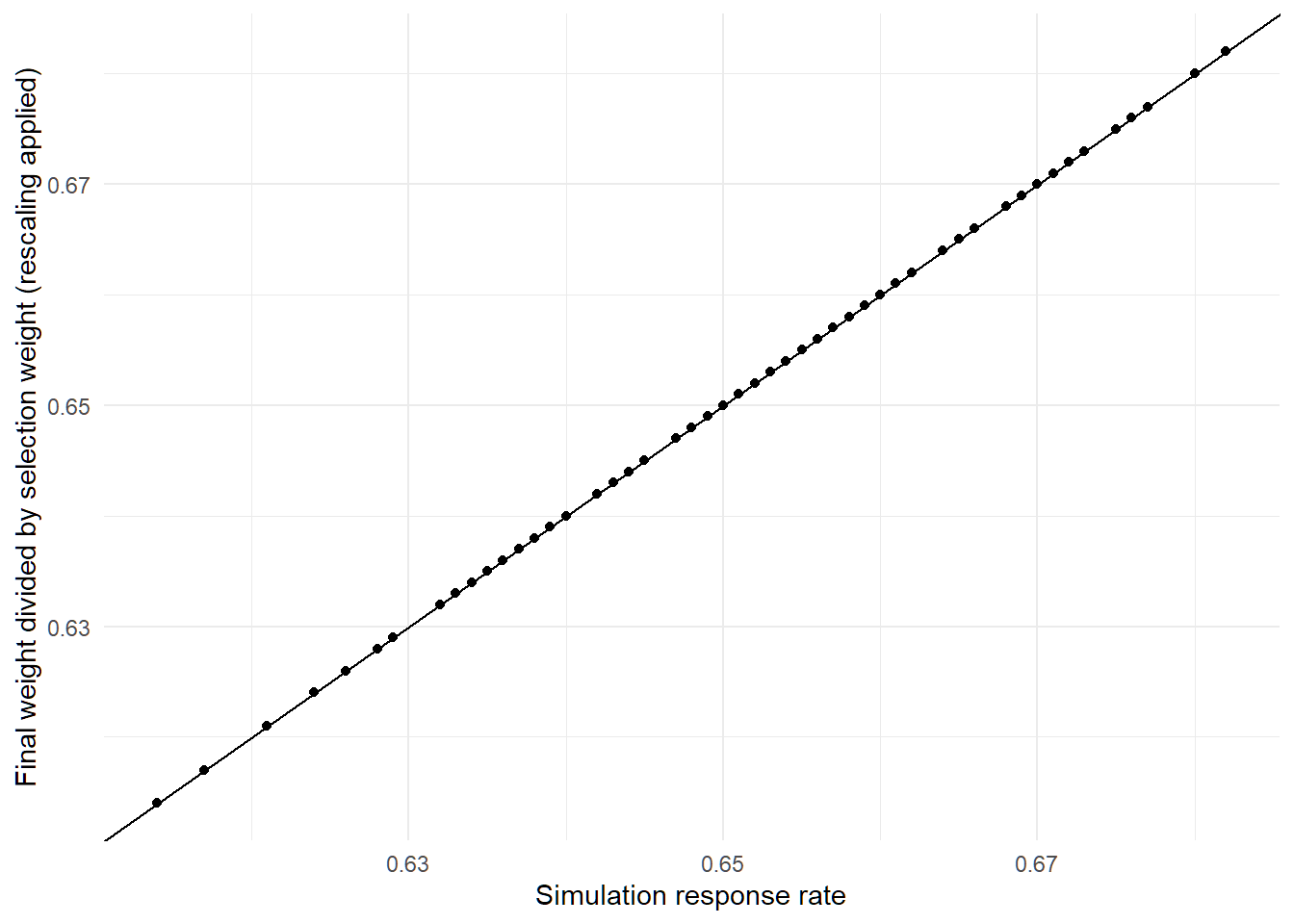
Apparently, that nails the minimum weight exactly. The mean absolute difference between this adjusted ratio and the response rate for the survey is just 0.0000000000000000621724893790088. At that point I’m willing to believe any remaining differences are just about floating point precision.
Does this work with different simulation parameters?
First of all, let’s make sure this actually holds up in a more complex simulation. I’ll set the poor response rate to 40% and say that people in bigger households are more likely to be rich (so that we have a correlation between selection probability and group response rates).
Apparently everything still works and the minimum of the adjusted ratios exactly matches the response rate.
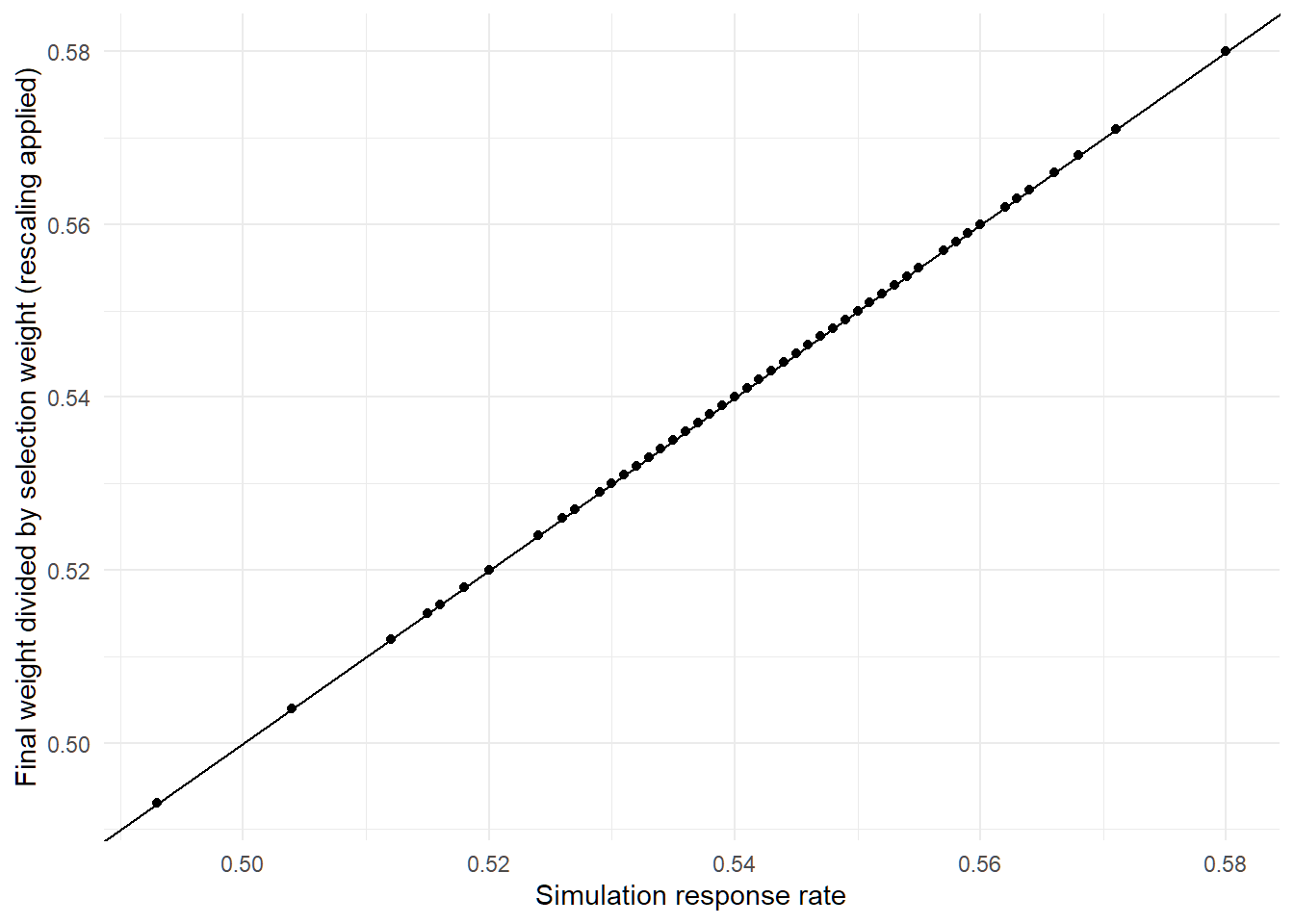
What about if I make the population 10 times larger?
Apparently this still works too:
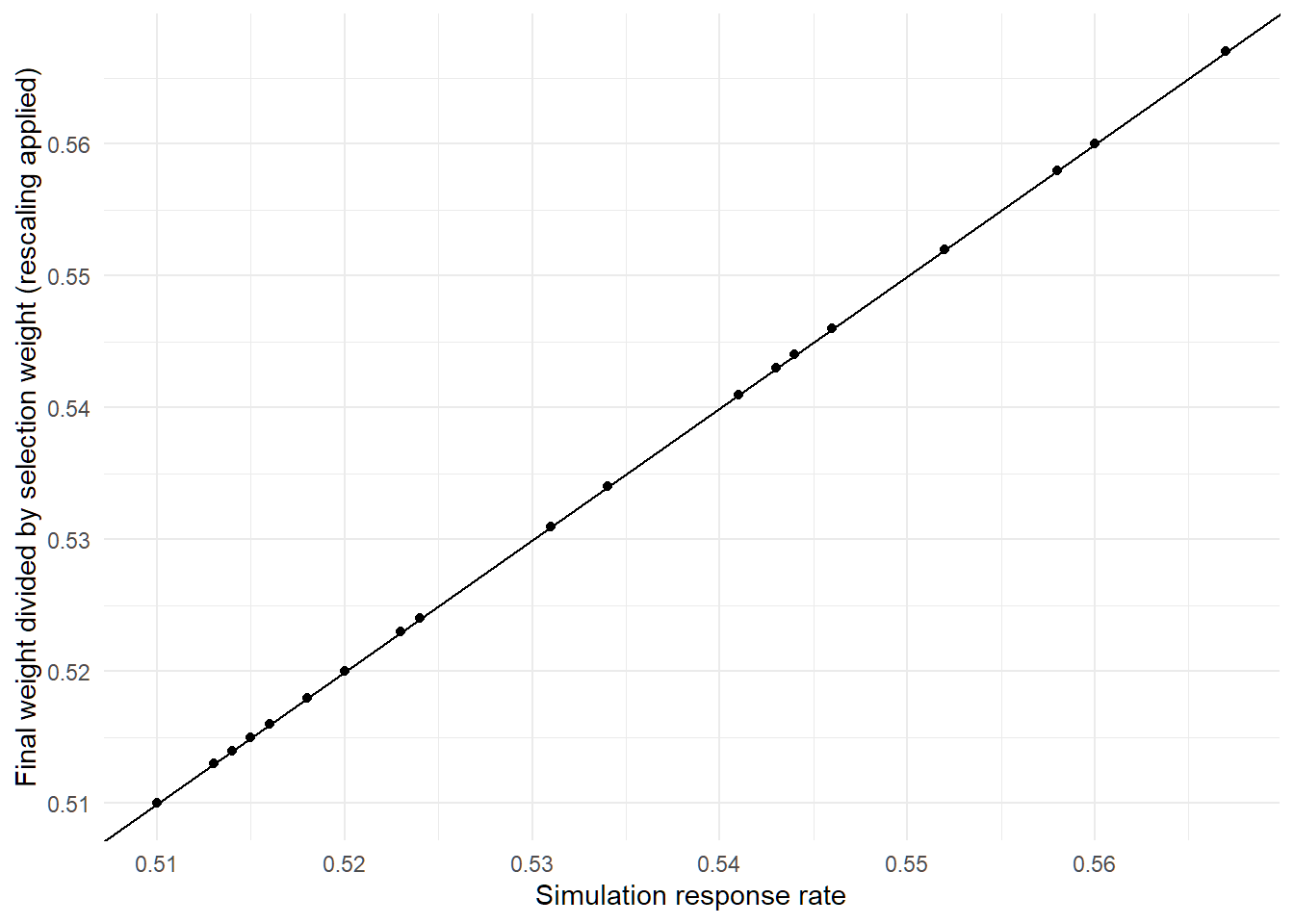
Summarizing the claim
So to formalize, the constraint is as follows. For each respondent, \(j\), define:
\[ r_j = \frac{FinalWeight_j}{SelectionWeight_j} \]
The adjusted ratio is defined as follows, where \(\bar{r}\) is the mean ratio across all respondents to the survey:
\[ r^{*}_j = \frac{r_j}{\bar{r}} \] Based on my simulations, it appears that:
\[ r^{*}_{j}>= RR_{total} \]
But why does this work?
🤷