The File Drawer
Do cluster robust standard errors give false positives on cross-level interactions?
One of the most easy traps to fall into in quantitative social science is fooling yourself (and your statistics software) into thinking you have more information about a question than you really do.
As always, this is best illustrated with an XKCD comic:
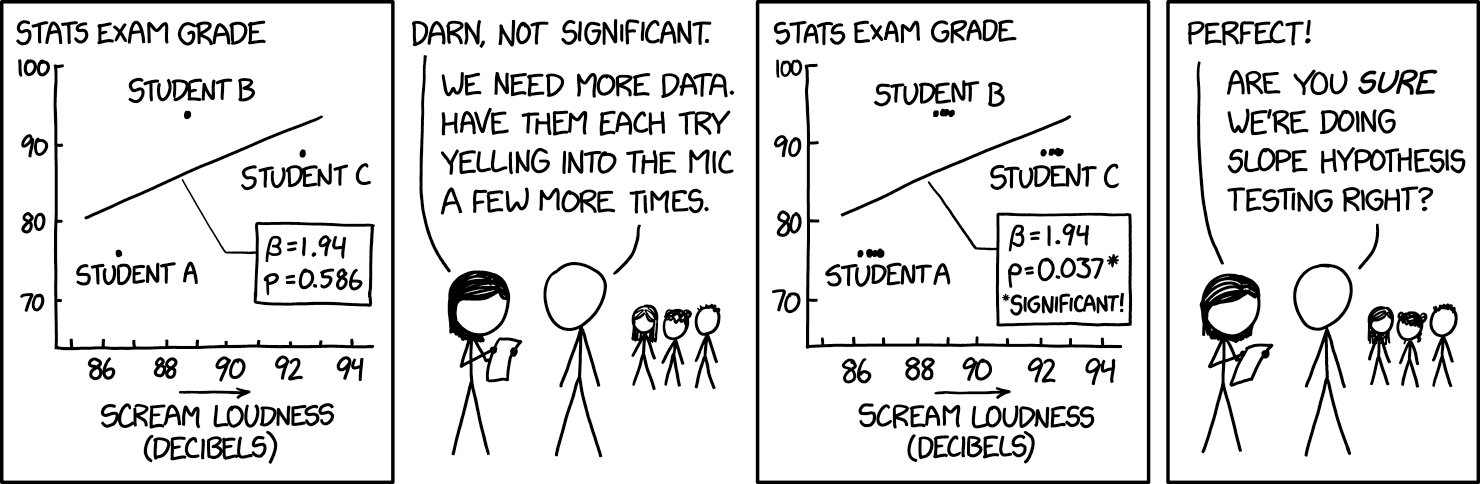
The key point here is that there are only really three independent pieces of information (the three students) and the multiple observations of their yelling are just repeated measurements of the same piece of information rather than new information. Taking the average of the yells for each student might increase the precision of that one datapoint, but it’s not new independent data. In fact, one of the variables in this example does not vary within students at all (stats exam grade). However, unless we tell the statistical software that this is the case, the default is to treat every row of a dataset as if it were independent information.
Studies usually account for this problem with some combination of cluster robust standard errors, fixed effects, and random effects models. All of these techniques have their detractors, but social scientists are generally aware that non-independent observations are important to account for.
A less commonly recognized version of this problem comes with cross-level interactions. To take a standard comparative political behavior type of question, suppose we have a study of 15,000 voters in 28 countries and we think that the effect of being in poverty on left-wing vote choice might depend on how generous the welfare state is.
The natural way to test this question is with a cross-level interaction between welfare state generosity and poverty. That model would look something like this, with a random intercept \(\alpha_{j}\) varying across countries:
\[ leftvote_{ij} = \alpha_{j} + \beta_1 \cdot poverty_i + \beta_2 \cdot welfarestate_j + \beta_3 \cdot poverty_i \cdot welfarestate_j + \epsilon_{ij} \]
In a 2019 paper, Heisig and Schaeffer show that this model is misspecified. The random intercept avoids the XKCD problem for \(\beta_2\) on the welfare state main effect, but does essentially nothing to help with the problem for \(\beta_3\) on the cross-level interaction. With only a random intercept, we’re essentially telling the model that we have 15,000 independent observations about how the slope of poverty varies across welfare states. But of course we don’t. The relationship between poverty and left wing voting undoubtedly varies for all sorts of reasons (or just idiosyncratically) across countries, so we may see a pattern that looks like a cross-level interaction by chance because the slopes in the 28 countries happen to vary in that way.
The solution is that for every cross-level interaction, you have to include a random slope \(\gamma_{j}\) for the lower-level variable.
\[ leftvote_{ij} = \alpha_{j} + \gamma_{j} \cdot poverty_i + \beta_1 \cdot poverty_i + \beta_2 \cdot welfarestate_j + \beta_3 \cdot poverty_i \cdot welfarestate_j + \epsilon_{ij} \] Worryingly, Heisig and Schaeffer find that most studies don’t include this interaction and that including it makes a lot of results insignificant!
This left me with a question though. Does the other major method of dealing with non-independent information (cluster robust standard errors) suffer from the same problem as a random intercepts model, or does clustering account for the non-independence of observations of the cross-level interaction?
When I come across questions like this, I usually turn to simulations. The advantage of a simulation approach is that you can find out whether something works (at least in a particular context) without having to dive into all of the underlying maths behind a technique.
So in my simulation, I specify a zero effect size for the cross-level interaction but have the slopes on the lower-level variable vary randomly across countries. I then fit four models to the simulated data: a standard lm, HLM with random intercepts, HLM with random intercepts and random slopes on the x-variable, and finally a cluster-robust linear model (lm.cluster from the miceadds package).
After doing that, these were the mean absolute t-statistics on the cross-level interaction for each method and the proportion of false positives:
| Prop. significant | Mean absolute t-stat | |
|---|---|---|
| lm | 0.900 | 13.9 |
| Random intercept | 0.900 | 13.9 |
| Random intercepts & slopes | 0.038 | 0.8 |
| Cluster robust SEs | 0.064 | 0.9 |
As expected, fitting the data using the standard lm function gives huge t-statistics on the cross-level interaction and random intercepts alone change essentially nothing. In both cases, we see around a 90% false positive rate which is pretty awful. As expected, Heisig and Schaeffer’s recommendation to use random slopes improves things a lot, with the false positive rate falling to around the 5% level expected.
Perhaps surprisingly, cluster robust standard errors get much closer to the random slope model’s performance, with only a 6% false positive rate. While that’s not quite the theoretical 5%, it makes me more confident that studies using cluster robust standard errors for cross-level interactions aren’t generating automatic false positives.
This is just one set of simulations, so I’m not making wider claims about these methods but this felt like a useful thing to share.